Sistem persamaan merupakan himpunan persamaan yang saling berhubungan. Dimana persamaan linear merupakan persamaan yang memuat variabel dengan menggunakan pangkat tertinggi sama dengan satu.
SPLDV adalah
Persamaan linear dari dua variabel berarti persamaan yang memuat dari dua variabel dengan adanya pangkat tertinggi 1. Sehingga sistem persamaan linear dua variabel bisa dipahami sebagai sebuah himpunan persamaan-persamaan linear yang memiliki dari dua variabel. Penyebutan pada nama sistem persamaan linear dua variabel sering disingkat sebagai SPLDV.
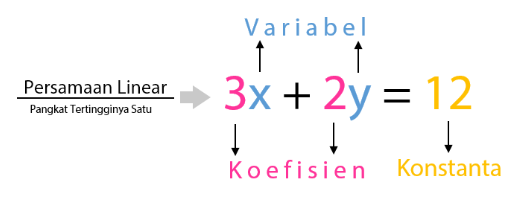
Sebuah persamaan linear sudah memiliki komponen yang meliputi variabel, koefisien, dan juga konstanta. Koefisien dan variabel terletak berdampingan dengan adanya tata letak koefisien di depan variabel. Konstanta pada persamaan linear berupa bilangan yang tidak diikuti oleh variabel. Contoh persamaan linear dari dua variabel adalah 3x + 2y = 12.
Bagaimana cara untuk menentukan solusi dari sistem persamaan linear dua variabel? Apa saja cara untuk menyelesaikan sistem persamaan linear pada dua variabel? kamu dapat mencari tahu jawabannya melalui ulasan cara menentukan solusi dari sistem persamaan dari linear dua variabel di bawah ini.
Bentuk Persamaan Linear
Persamaan linear dari dua variabel dengan memiliki karakteristik memiliki sebagai persamaan dengan adanya pangkat tertinggi dari semua variabel dalam persamaan adalah satu. Perhatikan adanya persamaan yang bukan SPLDV dan persamaan yang merupakan SPLDV sebagai berikut.
Cara Menyelesaikan Sistem Persamaan Linear Dua Variabel
Terdapat beberapa cara/metode agar bisa menyelesaikan permasalahan terkait Sistem Persamaan Linear Dua Variabel (SPLDV). Empat metode yang bisa digunakan adalah dengan menyelesaikan SPLDV adalah sebagai berikut.
- Substitusi
- Eliminasi
- Gabungan
- Grafik
Melalui halaman ini, sobat bisa mengetahui proses pengerjaan SPLDV dengan menggunakan berbagai metode. Untuk dapat mengetahui perbedaan setiap metode.
Permasalahan dalam SPLDV bisa diselesaikan dengan dua persamaan berikut.
(i) 2x + 3y = 8
(ii) 3x + y = 5
Metode Substitusi
Terdapat beberapa langkah yang perlu kamu lakukan agar bisa menyelesaikan SPLDV dengan adanya metode substitusi. Berikut ini terdapat langkah-langkah untuk menyelesaikan SPLDV dengan metode substitusi.
Langkah-langkah agar menyelesaikan SPLDV dengan metode substitusi sebagai berikut:
- Dengan adanya salah satu persamaan bisa menjadi bentuk y = ax + b atau x = cy + d [TRIK!! Pilihlah persamaan yang paling mudah agar dapat diubah]
- Substitusikanlah nilai x atau y yang dapat diperoleh dengan langkah pertama ke dalam persamaan yang lainnya.
- Selesaikanlah persamaan agar bisa mendapatkan nilai x atau y.
- Substitusikanlah nilai x atau y yang dapat diperoleh pada langkah ketiga dengan salah satu persamaan agar mendapatkan nilai dari variabel yang belum diketahui.
Metode Eliminasi
Cara kedua agar dapat menyelesaikan Sistem Persamaan Linear Dua Variabel dengan menggunakan metode eliminasi. Secara ringkas, dalam metode eliminasi bisa menghilangkan salah satu variabel agar mendapatkan nilai dari satu variabel lainnya.
Langkah-langkah untuk menyelesaikan Sistem Persamaan Linear Dua Variabel dengan menggunakan metode eliminasi:
- Menyamakan dari salah satu koefisien dari variabel x atau y pada kedua persamaan dengan cara mengalikan konstanta yang sudah sesuai.
- Hilangkanlah variabel yang memiliki koefisien yang sama dengan cara menambahkan atau dengan mengurangkan kedua persamaan.
- Ulangilah kedua langkah agar mendapatkan variabel yang belum kamu ketahui.
Metode Grafik
Penyelesaian Sistem Persamaan Linear Dua Variabel dengan menggunakan metode grafik dapat dilakukan dengan menentukan koordinat titik potong pada kedua garis yang mewakili dari kedua persamaan linear.
- Menggambar garis untuk mewakili kedua persamaan pada bidang kartesius
- Menemukan titik potong dari kedua grafik tersebut
Demikianlah ulasan mengenai Sistem Persamaan Linear Dua Variabel. Yuk belajar lebih giat lagi guys agar nilai kamu menjadi lebih baik. Terimakasih telah berkunjung dan SEE YAA!!!






