Rumus Kuartil Data Kelompok – Bagi kalian yang suka dengan pelajaran matematika pasti tidak asing dengan data, rumus dan hal sebagainya. Nah disini kami akan bahas mengenai Rumus Kuartil Data Kelompok.
Pengertian kuartil hampir sama dengan median. Hanya saja, pada kuartil pembagianya adalah empat. Kuartil adalah suatu nilai yang bisa membagi kumpulan data menjadi empat bagian sama besar.
Syarat untuk mendapatkan kuartil ini adalah data harus diurutkan terlebih dahulu. Oleh karena membagi data menjadi empat bagian sama besar, maka setiap bagian memilki persentase 25%.
Kuartil merupakan nilai yang membagi sekumpulan data yang urut menjadi empat bagian yang sama, yaitu bagian pertama, bagian kedua, bagian ketiga, dan juga bagian keempat.
Kuartil terbagi menjadi tiga yang didapat dari suatu gugus daya, yaitu kuartil 1 (Q1), kuartil 2 (Q2 atau median), dan kuartil 3 (Q3). Kuartil menjadi konsep yang secara konseptual terdapat di dalam statistik yang konsepnya mirip dengan median data tunggal.
Sehingga untuk memahaminya, sama halnya seperti kembali ke median yang mana menghitungnya dengan cara memotong data menjadi dua kelompok.
Dua kelompok yang datanya telah dipotong tadi memiliki jumlah yang sama dengan nilai tengah yang memisahkan kelompok tersebut atau yang kemudian disebut sebagai median.
Setelah itu, dengan cara yang sama, data kembali dibagi menjadi 4 kelompok yang sama dengan pembeda pertama adalah kuartil pertama dan titik kedua yaitu kuartil kedua, dan seterusnya.
Jika secara umum sudah dijelaskan bahwa kuartil adalah sekumpulan data yang urut menjadi empat bagian yang sama, yaitu bagian pertama, bagian kedua, bagian ketiga, dan juga bagian keempat, maka ada beberapa ahli yang memiliki sudut pandang masing-masing mengenai apa itu kuartil.
- Menurut Wirawan (2001: 105),pengertian kuartil atau (K) adalah nilai-nilai yang membagi serangkaian data atau suatu distribusi frekuensi menjadi empat bagian yang sama. Ada tiga kuartil, yaitu kuartil pertama (K1), kuartil kedua (K2), dan kuartil ketiga (K3).
- Sementara itu, ahli lain yang bernama Sudijono (2006: 112) mengungkapkan bahwa kuartil adalah titik atau skor atau nilai yang membagi seluruh distribusi frekuensi ke dalam empat bagian yang sama besar.
Yaitu masing-masing bagian sebesar seperempat. Sehingga di sini akan dijumpai tiga buah kuartil, yaitu kuartil pertama (K1), kuartil kedua (K2), dan kuartil ketiga (K3).
- Suliyanto (2002: 106)berpendapat bahwa kuartil berarti membagi kelompok data menjadi empat bagian, yaitu bagian pertama sampai bagian keempat.
- Selain itu, menurut Sudjana (2005: 81)jika sekumpulan data dibagi menjadi empat bagian yang sama banyak, sesudah disusun menurut urutan nilainya, maka bilangan pembaginya disebut kuartil.
Ada tiga buah kuartil, ialah kuartil pertama, kuartil kedua, dan kuartil ketiga yang masing-masing disingkat dengan K1, K2, dan K3. Pemberian nama ini dimulai dari urutan kuartil yang paling kecil.
Apa itu Kuartil?
Kuartil adalah salah satu ukuran statistik yang digunakan untuk membagi data dalam empat bagian yang sama. Dalam konteks data kelompok, rumus kuartil memungkinkan kita untuk mengetahui batasan-batasan ini. Terdapat tiga jenis kuartil yang umum digunakan, yaitu kuartil bawah (Q1), kuartil tengah (Q2), dan kuartil atas (Q3).
Rumus Kuartil Data Kelompok
Untuk menghitung kuartil pada data kelompok, kita harus mengikuti beberapa langkah yang jelas. Berikut adalah rumus-rumus yang dapat Anda gunakan:
1. Menghitung Kuartil Bawah (Q1)
Kuartil bawah (Q1) adalah batas pertama yang membagi data menjadi 25% dan 75%. Untuk menghitungnya, ikuti langkah-langkah berikut:
- Urutkan data kelompok secara terurut meningkat.
- Hitung persentase persentil ke-25 (P25).
- Temukan nilai dengan persentase persentil ke-25 dalam data kelompok yang telah diurutkan. Ini akan menjadi kuartil bawah (Q1).
2. Menghitung Kuartil Tengah (Q2)
Kuartil tengah (Q2) adalah median atau kuartil ke-50 yang membagi data menjadi 50% dan 50%. Untuk menghitungnya, ikuti langkah-langkah berikut:
- Urutkan data kelompok secara terurut meningkat.
- Hitung persentase persentil ke-50 (P50).
- Temukan nilai dengan persentase persentil ke-50 dalam data kelompok yang telah diurutkan. Ini akan menjadi kuartil tengah (Q2).
3. Menghitung Kuartil Atas (Q3)
Kuartil atas (Q3) adalah batas kedua yang membagi data menjadi 75% dan 25%. Untuk menghitungnya, ikuti langkah-langkah berikut:
- Urutkan data kelompok secara terurut meningkat.
- Hitung persentase persentil ke-75 (P75).
- Temukan nilai dengan persentase persentil ke-75 dalam data kelompok yang telah diurutkan. Ini akan menjadi kuartil atas (Q3).
Contoh Penggunaan Rumus Kuartil
Mari kita lihat contoh penggunaan rumus kuartil pada data kelompok berikut:
| Kelompok | Frekuensi |
|---|---|
| 1-10 | 5 |
| 11-20 | 10 |
| 21-30 | 15 |
| 31-40 | 8 |
| 41-50 | 12 |
Menghitung Kuartil Bawah (Q1)
- Urutkan data kelompok secara terurut meningkat:
- 1-10, 11-20, 21-30, 31-40, 41-50
- Hitung persentase persentil ke-25 (P25):
- P25 = (25/100) * N
- P25 = (25/100) * 50
- P25 = 12.5
- Temukan nilai dengan persentase persentil ke-25 dalam data kelompok yang telah diurutkan:
- Q1 = 21-30
Menghitung Kuartil Tengah (Q2)
- Urutkan data kelompok secara terurut meningkat:
- 1-10, 11-20, 21-30, 31-40, 41-50
- Hitung persentase persentil ke-50 (P50):
- P50 = (50/100) * N
- P50 = (50/100) * 50
- P50 = 25
- Temukan nilai dengan persentase persentil ke-50 dalam data kelompok yang telah diurutkan:
- Q2 = 31-40
Menghitung Kuartil Atas (Q3)
- Urutkan data kelompok secara terurut meningkat:
- 1-10, 11-20, 21-30, 31-40, 41-50
- Hitung persentase persentil ke-75 (P75):
- P75 = (75/100) * N
- P75 = (75/100) * 50
- P75 = 37.5
- Temukan nilai dengan persentase persentil ke-75 dalam data kelompok yang telah diurutkan:
- Q3 = 41-50
Dalam contoh ini, kuartil bawah (Q1) adalah 21-30, kuartil tengah (Q2) adalah 31-40, dan kuartil atas (Q3) adalah 41-50.
Rumus Kuartil Data Kelompok
Data berkelompok adalah kumpulan data yang ditulis dalam bentuk interval. Kuartil data berkelompok adalah suatu nilai yang membagi data-data interval menjadi empat bagian sama besar.
Penggunaan rumus pada kuartil data tunggal dan kuartil data berkelompok tentu saja berbeda. Oleh sebab itu, Anda harus memahami rumus-rumus tersebut dengan jeli agar dapat menerapkannya dengan tepat.
Perlu diketahui, jika rumus pada kuartil data tunggal tersebut adalah disajikan dengan cara sederhana dan belum dikelompokkan pada kelas interval.
Sementara itu rumus pada kuartil data berkelompok ini adalah data yang sudah disajikan dalam bentuk tabel frekuensi dan biasanya sudah dikelompokkan dalam kelas interval.
Berikut adalah rumus kuartil data berkelompok.
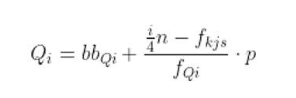
Keterangan :
i = kuartil ke-i
bbQi = batas bawah kelas kuartil ke-i
n = banyaknya data
fkjs = frekuensi kumulatif sebelum kelas kuartil ke-i
fQi = frekuensi kelas kuartil ke-i
p = panjang kelas
Rumus Kuartil Data Tunggal
Rumus Kuartil pada Data Tunggal
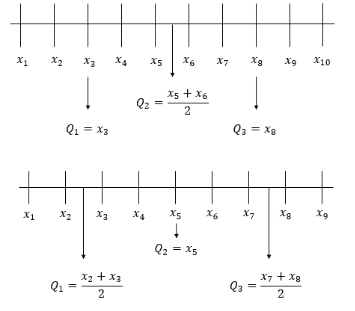
Quartil Data Tunggal (Arsip Zenius)
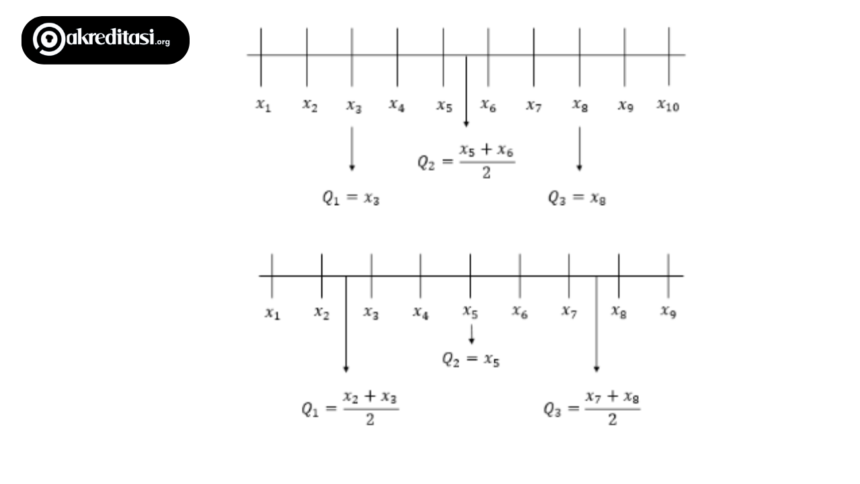
Jika data sudah terlalu banyak untuk diurutkan, kalian bisa menggunakan rumus-rumus berikut untuk mengetahui letak kuartilnya.
Rumus Kuartil Data Tunggal jika Data Ganjil
Kuartil untuk n+1 habis dibagi 4
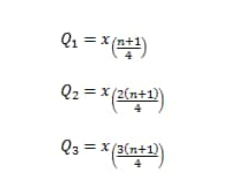
Kuartil untuk n+1 tidak habis dibagi 4
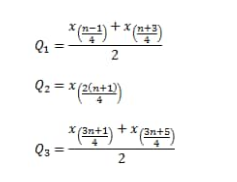
Rumus Kuartil Data Tunggal jika Data Genap
Jika data habis dibagi 4
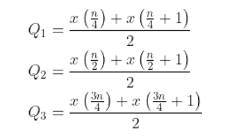
Jika data tidak habis dibagi 4
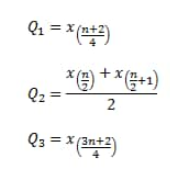
Rumus Kuartil pada Data Kelompok
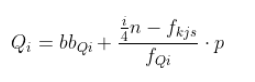
i = kuartil ke-i
bbQi = batas bawah kelas kuartil ke i
n = banyaknya data
fkjs = frekuensi kumulatif sebelum kelas kuartil ke-i
fQi = frekuensi kelas kuartil ke-i
p = panjang kelas
Biar lebih mudah memahami materi dan rumus kuartil, kita langsung aja coba dengan contoh soal kuartil data kelompok, yuk!
Contoh Soal dan Pembahasan
Soal 1
Sekarang coba elo perhatian contoh soal kuartil yang pertama.
Jika ada data berjumlah 123, tentukanlah letak kuartilnya!
Jawab:
Dari soal di atas, kita tidak punya informasi mengenai nilai terkecil, nilai terbesar, dan interval data.
Artinya, soal di atas meminta kita untuk menentukan letak kuartil dengan rumus cara mencari kuartil data tunggal.
Karena jumlah data ganjil dan jika n + 1 dapat dibagi habis dengan 4, maka rumus yang digunakan dan cara menjawabnya sebagai berikut.
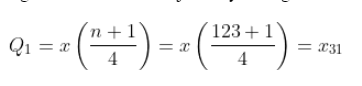
Soal 2
Dari data berjumlah 97, tentukanlah letak kuartilnya!
Jawab :
Sama seperti contoh soal kuartil yang pertama, yang diminta dicari pada soal kedua adalah letak kuartilnya. Karena jumlah data ganjil dan jika n + 1 tidak dapat dibagi habis dengan 4, maka rumus yang digunakan dan cara menjawabnya sebagai berikut.
Soal 3
Dari data berjumlah 200, tentukanlah letak kuartilnya!
Jawab:
Karena jumlah data genap dan bisa dibagi habis dengan 4, maka rumus yang digunakan dan cara menjawabnya sebagai berikut :
Rumus Kuartil Data Tunggal jika Data Ganjil
Kuartil untuk n+1 habis dibagi 4
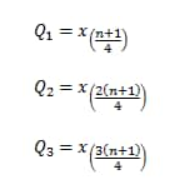
Kuartil untuk n+1 tidak habis dibagi 4
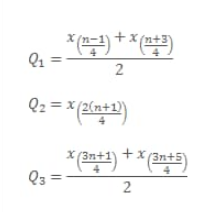
Rumus Kuartil Data Tunggal jika Data Genap
Jika data habis dibagi 4
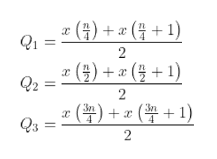
Jika data tidak habis dibagi 4
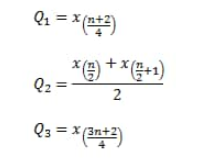
Nah itulah informasi mengenai Rumus Kuartil Data Kelompok, semoga informasi yang kami bagikan ini bermanfaat dan terima kasih telah membaca.