Garis dan sudut merupakan salah satu materi yang menjadi dasar untuk mempelajari materi-materi geometri yang lain. Dengan memahami konsep garis dan sudut, kalian akan dapat dengan mudah mempelajari konsep bidang, bangun datar, dan materi geometri yang lainnya.
Sebenarnya titik, garis, dan bidang dalam geometri tidak memiliki definisi atau pengertian yang pasti (mutlak). Akan tetapi untuk memudahkan pemahaman mengenai hal tersebut, terdapat beberapa istilah tidak formal yang digunakan.
Garis dapat didefinisikan sebagai kumpulan/himpunan titik-titik yang berjejer dan terhubung secara kontinu. Selanjutnya akan dibahas mengenai penerapan garis dalam kehidupan sehari-hari.
Garis dalam Kehidupan Sehari-Hari Banyak sekali penerapan garis dalam kehidupan sehari-hari. Bentuk-bentuk geometris banyak menerapkan konsep garis dalam pembuatannya.
Selain itu, dalam mempelajari persamaan garis, dapat menerapkan konsep garis untuk membantu dalam visualisasi garis pada koordinat kartesius.
Sudut adalah suatu objek geometri yang tersusun dari dua sinar garis dengan kedua pangkal sinar garis tersebut bertemu pada satu titik.
Kedua sinar garis tersebut merupakan kaki-kaki sudut dan titik pertemuan kedua pangkal sinar garis merupakan titik sudut. Selanjutnya akan dijelaskan mengenai jenis-jenis sudut.
1. Definisi Garis dan Sudut
Sebelum kita membahas lebih lanjut tentang penggunaan garis dan sudut, penting bagi kita untuk memahami definisi dasar dari kedua konsep ini.
1.1 Garis
Garis adalah objek matematika yang terdiri dari titik-titik yang terus berlanjut tanpa berhenti ke arah yang berlawanan. Garis tidak memiliki lebar atau panjang tertentu, dan dapat digambarkan sebagai rangkaian titik yang tak terhingga.
1.2 Sudut
Sudut adalah ruang antara dua garis yang berpotongan pada satu titik yang sama. Sudut diukur dalam satuan derajat atau radian, dan dapat berupa sudut tumpul, sudut lancip, atau sudut siku-siku, tergantung pada ukurannya.
2. Jenis-jenis Garis dan Sudut
Dalam matematika, terdapat berbagai jenis garis dan sudut yang memiliki karakteristik dan sifat yang berbeda. Berikut adalah beberapa jenis yang umum:
2.1 Jenis-jenis Garis
- Garis Lurus: Garis yang terus berlanjut tanpa berbelok.
- Garis Melengkung: Garis yang memiliki lengkungan atau kelengkungan.
- Garis Horizontal: Garis yang sejajar dengan sumbu x pada koordinat kartesian.
- Garis Vertikal: Garis yang sejajar dengan sumbu y pada koordinat kartesian.
- Garis Miring: Garis yang tidak sejajar dengan sumbu x atau y.
2.3 Jenis-Jenis Sudut
Pada bagian ini akan dijelaskan mengenai jenis-jenis sudut berdasarkan besar sudutnya.
- Sudut lancip
Perhatikan gambar berikut.
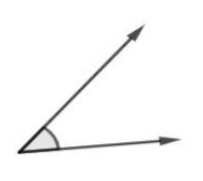
Sudut lancip merupakan jenis sudut dengan ukuran sudut antara 0° – 90° (kurang dari 90°).
- Sudut siku-siku
Perhatikan gambar berikut.
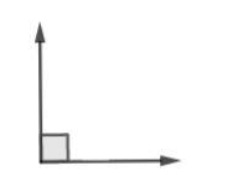
Pada gambar di atas terdapat sudut siku-siku. Sudut siku-siku memiliki besar sudut 90°.
- Sudut tumpul
Perhatikan gambar berikut.
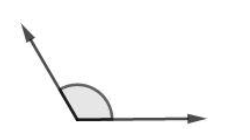
Sudut tumpul merupakan salah satu jenis sudut dengan ukuran sudut lebih dari 90° dan kurang dari 180°.
- Sudut lurus
Perhatikan gambar berikut.
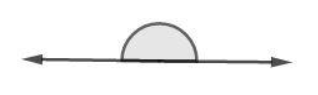
Gambar di atas merupakan sudut lurus dengan besar sudut 180°.
- Sudut refleks
Perhatikan gambar berikut.
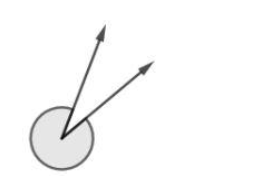
Gambar di atas merupakan gambar sudut refleks. Sudut refleks memiliki besar sudut lebih dari 180° dan kurang dari 360°.
Sifat-Sifat Sudut
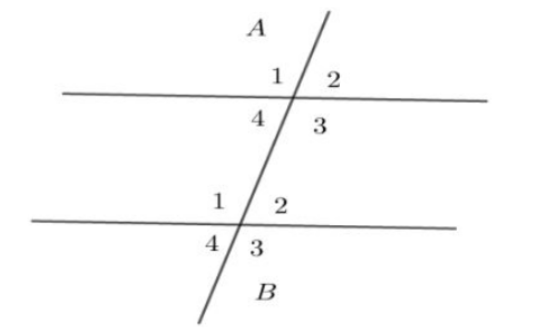
Perhatikan gambar berikut. Terdapat delapan sudut yang setiap sudutnya memiliki nama sudut beserta kode sudut yaitu A1, A2, A3, A4, B1, B2, B3, dan B4. Sudut-sudut tersebut memiliki hubungan antar satu sudut dengan sudut lainnya.
Sudut Luar Sepihak
Sudut ini memiliki jumlah sudut luar sepihak yaitu 180°.
Contoh: A1 dan A4, A2 dan B3.
Sudut Berpelurus
Memiliki jumlah besar sudut yang berpelurus yaitu sebesar 180°.
Contoh: A1 dan A2, A3 dan A4, B1 dan B2, B3 dan B4.
Sudut Bertolak Belakang
Sudut ini memiliki besar dua sudut yang bertolak belakang yang sama.
Contoh: A1 dan A3, A2 dan A4, B1 dan B3, B2 dan B4.
Sudut Sehadap
Kedua sudutnya memiliki sudut sehadap yang sama, maka dari itu sudut ini dikenal dengan istilah sudut sehadap.
Contoh: A1 dan B1, A2 dan B2, A3 dan B3, A4 dan B4.
Sudut Dalam Sepihak
Jumlah sudut dalam sepihak yaitu sebesar 180°.
Contoh: A4 dan B1, A3 dan B2.
Sudut Luar Berseberangan
Memiliki besar sudut luar berseberangan yang sama, sudut ini bernama sudut luar berseberangan.
Contoh: A1 dan B3 dan A2 dan A4.
Sudut Dalam Berseberangan
Sesuai namanya, sudut dalam berseberangan memiliki besar sudut dalam berseberangan yang sama.
Contoh: A4 dan B2 dan A3 dan B1.
Garis dan Sudut Rumus
Jika berdasarkan pengertian garis dan sudut kita bisa ambil kesimpulan, bahwa garis dan sudut tidak memiliki rumus, tetapi kalian bisa memahami melalui contoh yang kami berikan di bawah ini .
Contoh soal dan pembahasan garis dan sudut
- Jika besar sudut B2 adalah 75°, tentukan berapa besar sudut sudut A3!
Jawaban: Sudut B2 dan sudut A3 ialah merupakan dua sudut dalam sepihak yang memiliki jumlah 180°, sehingga besar sudut B2 ialah 180° – 75° = 105°.
Jadi, besar sudut pada A3 adalah 105°.
- Perhatikan gambar berikut
Tentukan hubungan antara sudut-sudut berikut berdasarkan pada gambar di atas!
- Sudut A1 dan sudut B3.
- Sudut A3 dan sudut B1.
- Sudut A2 dan sudut A4.
- Sudut B4 dan sudut A4.
Jawaban:
- Sudut luar yang berseberangan
- Sudut dalam yang berseberangan
- Sudut yang bertolak belakang
- Sudut saling sehadap
Nah itulah informasi yang bisa kami bagikan mengenai Garis dan Sudut, semoga informasi yang kami bagikan ini bermanfaat dan terima kasih telah membaca.