Matriks Transpose – Transpose matriks merupakan matriks baru yang elemen baris dan kolomnya merupakan elemen kolom dan baris matriks sebelumnya. Artinya, transpose matriks dibentuk oleh pembalikan elemen baris menjadi kolom dan elemen kolom menjadi baris.
Jika matriks yang akan dijadikan transpose bukan matriks persegi, maka ordo pada transposenya merupakan kebalikan dari ordo matriks sebelumnya.
Misalnya, matriks ordo 2 x 3 memiliki transpose matriks yang ordonya 3 x 2, matriks 3 x 1 memiliki transpose matriks yang ordonya 1 x 3, dan seterusnya.
Namun, jika bentuknya matriks persegi, transpose matriksnya tetap, misal matriks 2 x 2 memiliki transpose matriks 2 x 2, matriks 3 x 3 memiliki transpose matriks 3 x 3, dan seterusnya.
Ukuran matriks ditentukan berdasarkan jumlah baris dan kolom yang dimilikinya. Matriks dengan m kolom dan n baris disebut dengan matriks m x n, yang mana m dan n disebut dengan dimensinya.
Misalnya matriks di atas disebut dengan matriks 2 x 3. Hal tersebut disebabkan, matriks tersebut terdiri dari 2 baris dan 3 kolom.
Matriks dengan jumlah baris dan kolom yang sama disebut dengan matriks persegi. Adapun matriks dengan jumlah satu baris disebut dengan vektor baris. Sedangkan, matriks dengan satu kolom disebut dengan vektor kolom.
Adapun matriks tak terbatas merupakan matriks dengan jumlah baris atau kolom yang tak terbatas (atau keduanya). Pada beberapa konteks matriks yang dipertimbangkan tanpa baris atau tanpa kolom disebut dengan matriks kosong.
Matriks Transpose 2×2
Rumus determinan matriks ordo 2×2 Dilansir dari Chemistry LibreTexts, determinan matriks adalah penjumlahan dari semua hasil kali (permutasi) yang mungkin dari n elemen yang diambil dari baris dan kolom yang berbeda. Determinan berkaitan dengan ukuran matriks.
Makin besar ukuran matriks, maka makin kompleks cara mencari determinannya. Matriks ordo 2×2 merupakan matriks paling sederhana, sehingga cara mencari determinannya juga sederhana.
Determinan matriks ordo 2×2 dicari dengan cara mengalikan silang (diagonal) dari kiri atas ke kanan bawah lalu menguranginya dengan hasil kali elemen kanan atas dan kiri bawah
Tidak ada syarat khusus dalam pengerjaan transpose matriks baik itu matriks berordo 2 x 2 ataupun 3 x 3. Namun, terdapat perbedaan dari hasil transposenya . Contohnya Matriks A berdordo 2 x 3 , maka jika ditanspose akan menghasilkan matriks berordo 3×2 .
Beberapa sifat matriks transpose yaitu :
- (A+B)T = AT + BT
- (AT) = A
- k(AT) = (kA)T
- (AB)T = BT AT
Transpose Matriks Berordo 2 x 2
Cara menyelesaikan transpose matriks berordo 2 x 2 yaitu :
Tentukan lah transpose dari Matriks A dibawah ini !
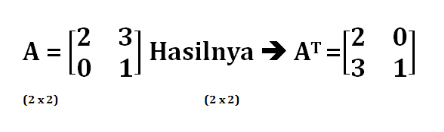
Matriks AT yaitu Baris menjadi kolom atau kolom menjadi baris dan tetap menghasil matriks berordo 2 x 2.
Contoh soal transpose matriks diatas juga merupakan pembuktian dari sifat matriks transpose (AT) = A . Jika ditukar posisinya hasil dari Matriks AT sama dengan Matriks A.
Matriks Transpose 2×3
Transpose Matriks Berordo 2 x 3
Contoh Transpose Matriks berordo 2 x 3 yaitu :
Tentukanlah transpose dari Matriks B dibawah ini :

Pada awalnya Matriks B berordo 2 x 3 setelah di transpose maka Matriks BT menghasilkan ordo 3 x 2 .
Contoh Transpose Matriks
1.Diketahui Matriks A dan Matriks B. Transpose dari A x B adalah ….
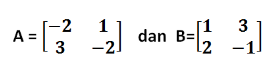
Gunakan perkalian matriks untuk mencari hasil [AB]. Hasilnya yaitu :
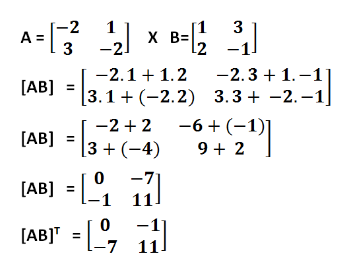
- Berapakah Hasil dari Matriks (A+B)Tdibawah ini !
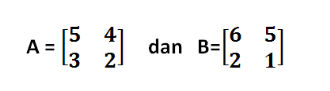
Penyelesaian :
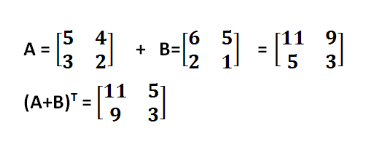
- Berapakah Hasil pengurangan dari matriks A – (BT)dibawah ini !
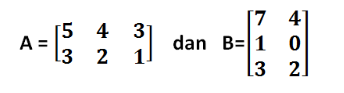
Penyelesaian :
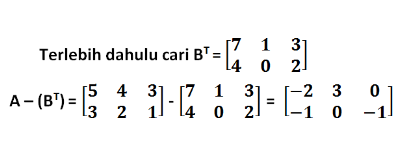
Nah itulah informasi yang bisa kami bagikan mengenai Matriks Transpose, semoga informasi yang kami bagikan ini bermanfaat dan terima kasih telah membaca.



