Gambar Kekongruenan – Kekongruenan atau kongruen merupakan konsep yang sering kita temukan dalam teori bilangan, aljabar, dan geometri. Dua objek dikatakan kongruen apabila mempunyai sifat yang sama atau setara.
Namun kongruensi bukanlah kesetaraan absolut antara dua objek, tetapi kesetaraan relatif dalam konteks tertentu, tergantung pada modulus yang digunakan.
Konsep kongruen tidak hanya untuk bilangan namun juga banyak diaplikasikan pada berbagai objek lainnya. Dalam geometri misalnya, dua bangun dikatakan kongruen jika mereka memiliki ukuran dan bentuk yang sama.
Begitu juga dalam materi pelajaran aljabar, kita dapat berbicara tentang kongruensi polynomial. Seperti, dua polinomial bisa dikatakan kongruen apabila koefisien mereka adalah sama.
Dalam konteks bilangan bulat, dua bilangan dikatakan kongruen modulo n jika mereka memiliki sisa yang sama setelah dibagi dengan n. Notasi yang digunakan untuk menyatakan kongruensi adalah ≡ (tanda tiga garis lurus).
Misalnya, jika a dan b adalah dua bilangan bulat, maka a ≡ b (mod n) berarti bahwa a dan b memberikan sisa yang sama ketika dibagi dengan n. Dalam hal ini, n disebut sebagai modulus.
Sebagai contoh, mari kita ambil modulus 5. Jika a = 17 dan b = 12, maka a ≡ b (mod 5), karena keduanya memberikan sisa 2 ketika dibagi dengan 5. Dalam kasus ini, kita dapat mengatakan bahwa a dan b kongruen modulo 5.
Gambar kekongruenan dua segitiga
Dua segitiga akan kongruen jika sisi-sisi yang bersesuaian sama panjang dan sudut-sudut yang bersesuaian sama besar. Untuk membuktikan kekongruenan dua buah segitiga, Anda harus menghitung setiap panjang sisi dan besar sudut kedua segitiga tersebut.
Tentunya hal ini akan menyita waktu. Untuk cara yang lebih efektif, Anda cukup mengetahui syarat-syarat dua segitiga yang kongruen.
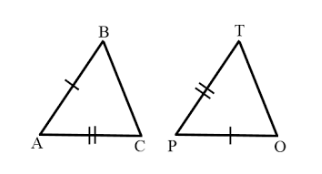
Kekongruenan
Suatu bangun dikatakan kongruen jika memenuhi syarat-syarat berikut.
- Besarnya sudut yang saling bersesuaian adalah sama.
- Perbandingan semua sisi yang saling bersesuaian bernilai satu karena panjangnya selalu sama
Kekongruenan pada Segitiga
Pada segitiga, kekongruenan bisa ditinjau dari urutan empat besaran, yaitu sisi-sudut-sisi, sudut-sisi-sudut, sisi-sisi-sisi, dan sisi-sudut-sudut. Artinya, Quipperian tidak perlu mengecek persamaan semua sisi dan sudutnya.
Gambar kekongruenan dan kesebangunan
Dua bangun dikatakan sebangun jika memenuhi dua syarat, yaitu sudut-sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian memiliki perbandingan yang sama.
Perhatikan gambar berikut.
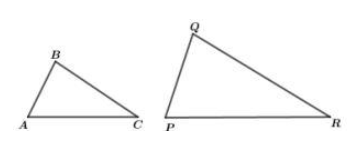
Pada gambar di atas terdapat dua segitiga yang sebangun.
Sudut-sudut yang bersesuaian yaitu susut ABC dengan sudut PQR, sudut ACB dengan sudut PRQ, dan sudut BAC dengan sudut QPR.
Sisi-sisi yang bersesuaian yaitu sisi AB dengan sisi PQ, sisi BC dengan sisi QR, dan sisi AC dengan sisi PR.
Sisi-sisi yang bersesuaian tersebut memiliki perbandingan yang sama.
Bagaimana dengan kekongruenan?
Bagaimana dua bangun dikatakan kongruen?
Dua bangun dikatakan kongruen jika memenuhi dua syarat, yaitu sudut-sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian memiliki ukuran yang sama.
Perhatikan gambar berikut.
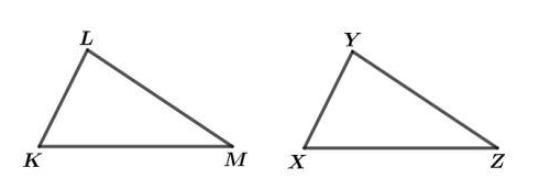
Pada gambar di atas terdapat dua segitiga yang kongruen.
Sudut-sudut yang bersesuaian yaitu sudut KLM dengan sudut XYZ, sudut KML dengan sudut XZY, dan sudut LKM dengan sudur YXZ.
Pada kedua bangun tersebut, sisi-sisi yang bersesuaian memiliki ukuran yang sama, yaitu sisi KL = sisi XY, sisi LM = sisi YZ, serta sisi KM = sisi XZ.
Kesebangunan Segitiga
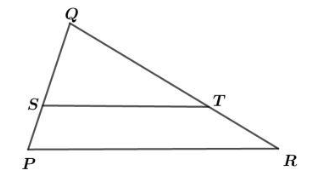
Pada gambar di atas terdapat dua bangun segitiga yaitusegitiga PQR dan segitiga QST.
Kedua segitiga tersebut sebangun, sehingga sudut-sudut yang bersesuaian sama besar.
Sudut-sudut yang bersesuaian yaitu sudut QPR dengan sudut QST, sudut PQR dengan sudut SQT, serta sudut QRP dengan sudut QTS.
Sisi-sisi yang bersesuaian juga memiliki perbandingan yang sama, yaitu sisi PR dengan sisi ST, sisi QP dengan QS, dan sisi QR dengan sisi QT.
Diperoleh perbandingan sebagai berikut.
PR/ST = QP/QS = QR/QT
Selanjutnya akan dijelaskan mengenai kesebagunan pada trapesium.
Kesebangunan Trapesium
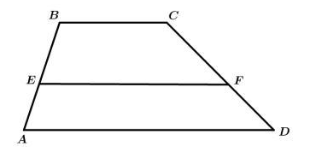
Pada gambar di atas terdapat dua trapesium yang sebangun.
Sudut-sudut yang bersesuaian memiliki besar sudut yang sama, yaitu sudut ABC dengan sudut EBC, sudut BCD dengan sudut BCF, sudut CDA dengan sudut CFE, serta sudut DAB dengan sudut FEB.
Sisi-sisi yang bersesuaian memiliki perbandingan yang sama, yaitu sisi AD dengan sisi EF, sisi AB dengan sisi EB, sisi CD dengan sisi CF, sehingga perbandingannya yaitu
AD/EF = AB/EB = CD/CF
Cara cepat untuk emnentukan ukuran EF yaitu sebagai berikut.
EF = ((BC x AE) + (AD x BE))/(AE + BE)
atau
EF = ((BC x FD) + (AD x CF))/(CF + FD)
Nah itulah informasi yang bisa kami bagikan mengenai Gambar Kekongruenan, semoga informasi yang kami bagikan ini bermanfaat dan terima kasih telah membaca.



