Rumus limit- Dalam matematika, konsep limit digunakan untuk menjelaskan perilaku suatu fungsi saat peubah bebasnya mendekati suatu titik tertentu, atau menuju tak hingga; atau perilaku dari suatu barisan saat indeks mendekati tak hingga.
Limit dipakai dalam kalkulus untuk membangun pengertian kekontinuan, turunan dan integral.
Pengertian Limit Fungsi
Limit fungsi adalah nilai yang dihasilkan oleh suatu fungsi ketika variabel yang terkait mendekati suatu nilai tertentu. Secara simbolis, limit fungsi dapat dituliskan sebagai berikut:
lim f(x) = L
x->a
Di mana f(x) adalah fungsi yang ingin dihitung limitnya, a adalah nilai yang variabel mendekati, dan L adalah nilai limit yang dihasilkan.
Cara Menghitung Limit Fungsi
Ada beberapa metode yang dapat digunakan untuk menghitung limit fungsi, di antaranya adalah:
Metode Substitusi Langsung
Metode ini digunakan ketika fungsi dapat langsung dihitung pada nilai yang dimaksud tanpa melakukan perhitungan tambahan. Untuk menggunakan metode ini, cukup substitusikan nilai yang dimaksud ke dalam fungsi dan hitung hasilnya.
Contoh:
Diberikan fungsi f(x) = 2x + 3. Hitunglah limit fungsi f(x) ketika x mendekati 2.
Penyelesaian:
Substitusikan x = 2 ke dalam fungsi f(x):
f(2) = 2(2) + 3 = 7
Sehingga, limit fungsi f(x) ketika x mendekati 2 adalah 7.
Metode Penyederhanaan
Metode ini digunakan ketika fungsi dapat disederhanakan menjadi bentuk yang lebih mudah untuk dihitung limitnya. Caranya adalah dengan melakukan operasi aljabar yang tepat untuk menyederhanakan fungsi.
Contoh:
Diberikan fungsi f(x) = (x^2 - 1) / (x - 1). Hitunglah limit fungsi f(x) ketika x mendekati 1.
Penyelesaian:
Menggunakan metode faktorisasi, kita dapat menyederhanakan fungsi menjadi:
f(x) = (x + 1)
Sehingga, limit fungsi f(x) ketika x mendekati 1 adalah 2.
Metode Aturan L’Hospital
Metode ini digunakan ketika fungsi menghasilkan bentuk tidak tentu seperti 0/0 atau ∞/∞ ketika nilai limit dihitung. Metode ini memanfaatkan aturan turunan untuk menghitung limit fungsi tersebut.
Contoh:
Diberikan fungsi f(x) = (e^x - 1) / x. Hitunglah limit fungsi f(x) ketika x mendekati 0.
Penyelesaian:
Terapkan aturan L‘Hospital dengan menghitung turunan pada pembilang dan penyebut fungsi:
f’(x) = (e^x) / 1 = e^x
Substitusikan x = 0 ke dalam turunan fungsi:
f‘(0) = e^0 = 1
Sehingga, limit fungsi f(x) ketika x mendekati 0 adalah 1.
Rumus limit tak hingga
Rumus limit tak hingga ini dapat dirumuskan seperti berikut:
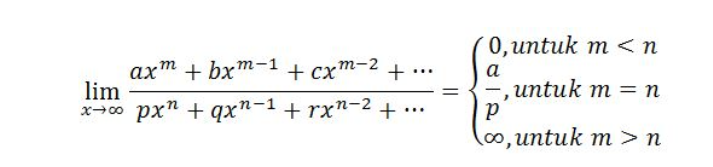
Agar anda lebih paham mengenai rumus limit tak hingga di atas. Maka saya akan membagikan contoh soal limit tak hingga terkait rumus tersebut. Adapun contoh soal dan pembahasannya yaitu:
Tentukan nilai limit tak hingga di bawah ini!
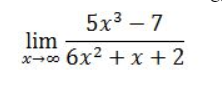
Pembahasan.
Dalam contoh soal ini kita dapat melihat bahwa pembilangnya memiliki pangkat tertinggi yang bernilai 3 (m), kemudian penyebutnya memiliki nilai pangkat paling tinggi berupa 2 (n). Maka dari itu nilai m > n, sehingga limitnya bernilai tak hingga (∞).
Rumus limit tak hingga akar
Rumus limit tak hingga akar dapat dirumuskan seperti berikut:
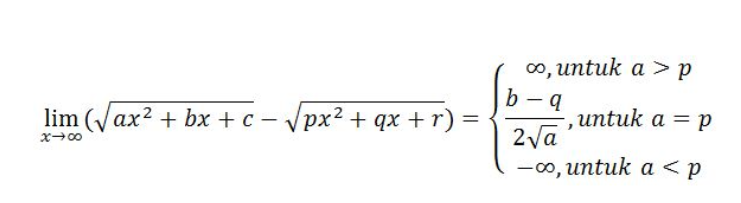
Contoh soal:
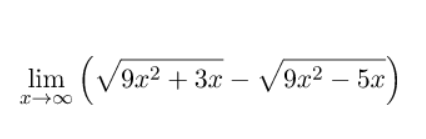
Nilai limit dari persamaan di atas adalah ….
A. 3/4
B. 4/5
C. 6/5
D. 5/4
E. 4/3
Jawab:
Soal limit di atas memiliki nilai a = p = 9, sehingga nilai limitnya dapat dicari menggunakan rumus:
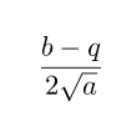
Perhatikan cara mendapatkan nilai limit tak hingga berikut.
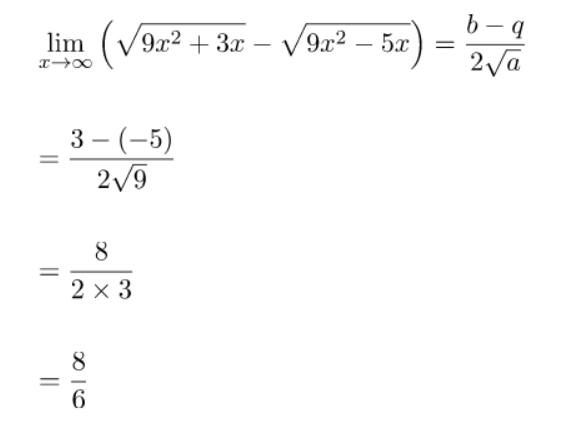
Jadi, nilai limit persamaan tersebut adalah 8/6 = 4/3.
Demikianlah teman-teman pembahasan kita hari ini tentang rumus limit, semoga bermanfaat dan jangan lupa di share ke teman-teman yang lain ya.



