Gambar Koordinat Pada Matematika – Hello sobat, kali ini kita kembali lagi dengan berita terbaru terkait dengan hal-hal menarik setiap harinya. Kali ini akan ada informasi mengenai Gambar Koordinat.
Gambar Koordinat Kartesius
Metode mudah yang sering digunakan untuk untuk menentukan posisi suatu benda adalah dengan menggunakan sistem koordinat.
Sistem koordinat dikenal sebagai suatu cara atau metode untuk menentukan letak suatu titik dalam grafik.
Bidang datar pada sistem koordinat disebut bidang koordinat yang dibentuk oleh garis tegak Y (sumbu Y) dan garis mendatar X (sumbu X).
Titik perpotongan antara garis Y dan X disebut pusat koordinat atau titik 0. Bidang koordinat tersebut dikenal dengan bidang koordinat Kartesius.
Bidang koordinat Kartesius digunakan untuk menentukan letak sebuah titik yang dinyatakan dalam pasangan bilangan.
Letak titik-titik tersebut dapat ditentukan dengan bergerak dari titik 0. Dilanjutkan dengan bergerak ke arah kanan mendatar (sumbu X), kemudian bergerak ke atas (sumbu Y).
Letak titik pada bidang koordinat Cartesius ditulis dalam bentuk pasangan bilangan (x, y) dengan x disebut absis dan y disebut ordinat. Berikut contoh simple pasangan x dan y.
– Titik A terletak pada koordinat (1. 1), ditulis A(1, 1).
– Titik B terletak pada koordinat (2, 3), ditulis B(2, 3).
– Titik C terletak pada koordinat (4, 2), ditulis (4. 2).
– Titik D terletak pada koordinat (5. 0), ditulis D(5, 0).
Bidang koordinat Kartesius dapat dibagi menjadi 4 kuadran.
- Kuadran 1
- Kuadran 2
- Kuadran 3
- Kuadran 4

Pemisah antarkuadran disebut sumbu koordinat. Pada sumbu koordinat terdapat sumbu mendatar (horizontal) dan sumbu tegak (vertikal). Perpotongan kedua sumbu koordinat disebut titik pangkal (titik pusat).
Setiap sumbu koordinat terbagi menjadi ukuran satuan yang selanjutnya disebut koordinat. Koordinat di sebelah kanan titik pangkal memiliki nilai positif, sumbu koordinatnya disebut sumbu X positif.
Koordinat di sebelah kiri titik pangkal memiliki nilai negatif, sumbu koordinatnya disebut sumbu X negatif. Koordinat di atas titik pangkal memiliki nilai positif, sumbu koordinatnya disebut sumbu Y positif.
Sementara itu, koordinat di bawah titik pangkal memiliki nilai negatif, sumbu koordinatnya disebut sumbu Y negatif.
Berikut cara-cara untuk menentukan koordinat
Diketahui koordinat titik P(-3, 4), Q(2, 4), R(2, -2), dan S(-3, -2).
- Gambarkan titik-titik tersebut ke dalam bidang koordinat!
- Jika keempat titik dihubungkan dengan ruas garis, bangun apa yang terbentuk?
Penyelesaian:
- Gambar titik-titik pada bidang koordinat seseuai dengan titik-titik yang diketahui
- Bangun PQRS merupakan bangun segi empat. Oleh karena jarak titik P dengan titik Q tidak sama dengan jarak titik Q dengan titik R maka PQRS merupakan bangun persegi panjang.’
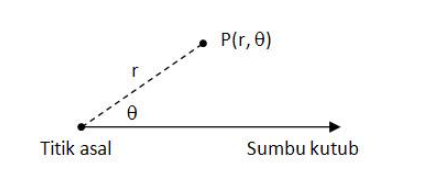
Gambar Koordinat Kutub
Sistem koordinat kutub dalam suatu bidang terdiri dari satu titik tetap O yang disebut titik asal atau titik kutub dan sebuah garis berarah yang bermula dari titik asal tersebut, yang disebut dengan sumbu kutub.
Dalam koordinat kutub, setiap titik P dinyatakan dalam pasangan (r, θ), di mana r adalah jarak titik P ke titik asal, dan θ adalah sudut dari sumbu kutub ke garis OP. Bilangan r disebut koordinat radial dan q disebut koordinat angular atau sudut kutub dari P.
Sudut dinyatakan dalam angka positif jika diukur berlawanan jarum jam dan dinyatakan dengan angka negatif jika diukur searah jarum jam.
Demikianlah informasi menarik kali ini mengenai Gambar Koordinat. Semoga bermanfaat dan menginspirasi.



