Polinomial Dalam Dunia Matematika – Hello sobat, kali ini kita kembali lagi dengan berita terbaru terkait dengan hal-hal menarik setiap harinya. Kali ini akan ada informasi mengenai Polinomial.
Polinomial Suku Banyak
Polinomial atau suku banyak merupakan pernyataan matematis yang berhubungan dengan jumlahan perkalian pangkat dalam satu atau lebih variabel dengan koefisien dalam dunia matematika.
Polinomial memiliki bentuk umum sebagai berikut:
anxn+…+a2x2+a1x1+a0
dimana a merupakan koefisien konstan, dan pangkat tertinggi pada polinomial tersebut menandakan orde atau derajatnya, sehingga polinomial diatas memiliki derajat atau orde n.
Pembagian Polinomial
Pada umumnya, bentuk umum dari pembagian polinomial adalah
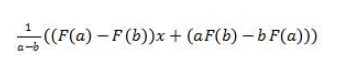
F(x) = P(x) × H(x) + S(x)
Dimana
F(x) : suku banyak
H(x) : hasil bagi
P(x) : pembagi
S(x) : sisa
Untuk memahami metode pembagian polinomial, kita harus mengetahui tentang teorema sisa.
Misalkan F(x) merupakan polinomial berderajat n,
Jika F(x) dibagi (x-k) maka hasilnya adalah F(k)
Jika F(x) dibagi (ax-b) maka hasilnya adalah F(b/a)
Jika F(x) dibagi (x-a)(x-b) maka hasilnya adalah
Berikut metode pembagian polinomial
- Metode Pembagian Biasa
Contohnya adalah jika 2×3 – 3×2 + x + 5 dibagi dengan 2×2 – x – 1
maka hasil bagi dan sisanya adalah hasil bagi = x-1 dan sisa = x+4
- Metode Horner
Metode ini dipakai untuk pembagi yang berderajat 1 ataupun pembagi berderajat n yang bisa difaktorkan jadi pembagi-pembagi dengan derajat 1.
Langkah-langkah :
- Tulis koefisien dari polinomialnya → harus urut dari koefisien xn, xn – 1, … hingga konstanta (untuk variabel yang tidak memiliki koefisien, maka ditulis 0). Misalkan untuk 5×3 – 8, koefisien-koefisiennya adalah 5, 0, 0, dan -8
- Untuk koefisien dengan derajat tertinggi P(x) ≠ 1, hasil baginya harus dibagi dengan koefisien derajat tertinggi P(x)
- Jika pembagi dapat difaktorkan menjadi
P1 dan P2, maka S(x) = P1 × S2 + S1
P1, P2, P3, maka S(x) = P1×P2×S3 + P1×S2 + S1
P1, P2, P3, P4, maka S(x) = P1×P2×P3×S4 + P1×P2×S3 + P1×S2 + S1
dan seterusnya
contoh :
F(x) = 2×3 – 3×2 + x + 5
P(x) = 2×2 – x – 1
Tentukan hasil bagi dan sisanya
Jawab :
F(x) = 2×3 – 3×2 + x + 5
P(x) = 2×2 – x – 1 = (2x + 1)(x – 1)
Sehingga p1 : (2x + 1) = 0 -> x = -1/2 dan p2 : (x – 1) = 0 -> x = 1
Polinomial Dalam Kehidupan Sehari Hari
Penerapan Polinomial dalam kehidupan sehari-hari sangat banyak. Roller coaster desainer dapat menggunakan polinomial untuk menggambarkan kurva dalam wahana mereka.
Kombinasi fungsi polinom kadang-kadang digunakan dalam ekonomi untuk melakukan analisis biaya, misalnya polinomial untuk pemodelan atau fisika Polinomial juga dapat digunakan untuk model situasi yang berbeda.
Di pasar saham untuk melihat bagaimana harga akan bervariasi dari waktu ke waktu. Bisnis orang juga menggunakan polinomial ke pasar model, seperti dalam untuk melihat bagaimana menaikkan harga barang akan mempengaruhi penjualan
Demikianlah informasi menarik kali ini mengenai Polinomial. Semoga bermanfaat dan menginspirasi.



